TL;DR

In this post, we introduce CARBS, a cost-aware hyperparameter optimizer that:

• Automatically reproduces the Chinchilla scaling law for LLMs from DeepMind, while also discovering scaling laws for every other hyperparameter, using significantly less compute, and being applicable to any deep learning problem (not just language models)

• Effectively solves OpenAI’s ProcGen benchmark just by properly tuning a very simple baseline model (PPO, as provided in the original ProcGen paper)

Hyperparameter tuning is massively impactful

Tuning simple baselines can lead to order-of-magnitude performance gains for the same amount of compute, particularly as models are scaled up. ^{1 2} Some studies have even suggested that the choice of hyperparameters can be more impactful than the choice of model. ³

Perhaps the most striking recent demonstration of the importance of hyperparameter tuning is the Chinchilla scaling laws study from DeepMind, which showed that a 70B parameter language model can outperform a 175B model simply by scaling a single hyperparameter (the number of training tokens). This discovery was transformative, enabling the next generation of large language models to be trained at a fraction of the cost.

But systematic tuning is seldom done, particularly on large models

Yet despite the proven value and an ever-growing zoo of hyperparameter tuners, most networks today are still not systematically tuned. In an informal survey of researchers presented at NeurIPS 2022, approximately three-quarters of respondents reported that they tune five or fewer hyperparameters and at least two-thirds stated that they use fewer than 25 tuning trials. According to the survey, nearly half of researchers perform tuning manually, while most of the other half use grid search or random search as their automated process, both of which are ill-suited to the task of exhaustively exploring hyperparameter configurations for large models.

This trend is highly concerning—aside from potentially missing out on important discoveries like the Chinchilla result, a lack of thorough tuning generally leads to suboptimal performance, unnecessary expense, and ambiguity when comparing new methods to the previous SOTA.

Why don’t people tune their networks?

There are a few main reasons why, despite the obvious benefit of tuning, it is so rarely done systematically in practice:

Large models are prohibitively expensive to evaluate

Even the most efficient tuning methods require occasionally evaluating the model. As deep learning models are scaled up, these evaluations become prohibitively expensive. The standard practice is to tune smaller models and then hope that those values are identical for larger models, or to use the hyperparameters of the smaller models as a “warm start” and do a minimal amount of additional tuning for larger models. However, there is considerable evidence that the optimal hyperparameters depend on scale ^{2 4 5} , and so these approaches do not actually yield the optimal hyperparameters for the larger model.

In order to effectively tune large models, the tuner must learn these complex scaling relationships, exploiting the rich statistical information gained from iterating on smaller models. It must also be aware of the cost associated with a given model, meaning that it understands and weighs the cost of training the model against its performance, finding the best-performing hyperparameters that are also the most compute-efficient.

Current methods struggle when there are many hyperparameters

Though there are several approaches to hyperparameter optimization, Bayesian optimization using Gaussian process surrogate models (see e.g. this review) has emerged as a primary tool thanks to its sample efficiency, flexibility, and robustness ^{6 7} . However, though Bayesian Optimization has been very successful on problems with a small number of parameters, it often performs poorly as the number of parameters grows ⁸ , in part because the search space grows exponentially; global acquisition functions tend to over-explore larger search spaces since there are more highly uncertain regions. For this reason, often only a small subset of hyperparameters are tuned in practice.

Tuning requires expert judgment calls about tradeoffs, budgets, and search bounds

The above constraints inhibit fully-automated hyperparameter tuning pipelines, as decisions about which subsets of hyperparameters to tune, how to balance performance against cost, and what scaling strategies to employ require considerable manual effort and expertise. In addition to being time-consuming, manual tuning by trial and error is fundamentally a bias-prone and irreproducible way of doing science.

Introducing CARBS

To overcome these limitations and provide a practical tool for robustly tuning hyperparameters, we present Cost-Aware pareto-Region Bayesian Search (CARBS). CARBS is a Bayesian Optimization algorithm that models both performance and cost (measured in GPU-hours) as Gaussian Proccesses and jointly optimizes them. CARBS learns an ever-improving model of the performance-cost Pareto frontier while searching locally in the neighborhood of this frontier. The local search allows CARBS to optimize even in unbounded search spaces with many parameters, which makes it much easier to use. By explicitly learning cost-dependent relationships, CARBS automatically models scaling relationships for every parameter as a byproduct of the tuning process. This also allows it to tune parameters such as the number of training epochs or training tokens, which are usually held constant in the tuning process—even though, as the Chinchilla result strikingly demonstrated, co-tuning these hyperparameters can drastically improve both the performance and efficiency of models.

CARBS is entirely automated and does not require specifying search bounds or training budgets. The goal is to automate much of the “black magic” of hyperparameter tuning. For more technical details and results, please refer to our preprint on arXiv. For the remainder of this blog post, we will highlight two dramatic results obtained with CARBS.

Demo 1 (Large Language Model): CARBS reproduces Chinchilla’s scaling laws as a bonus

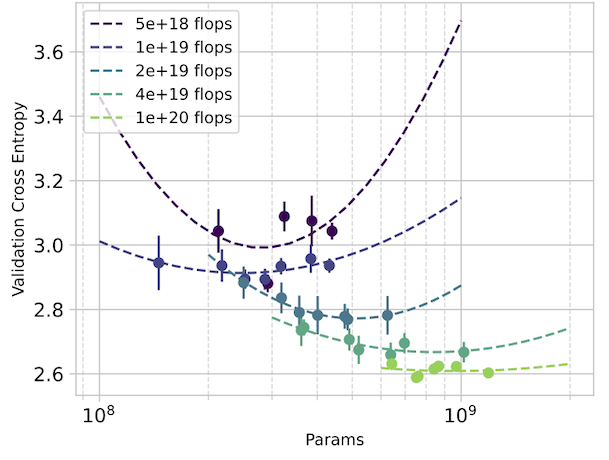
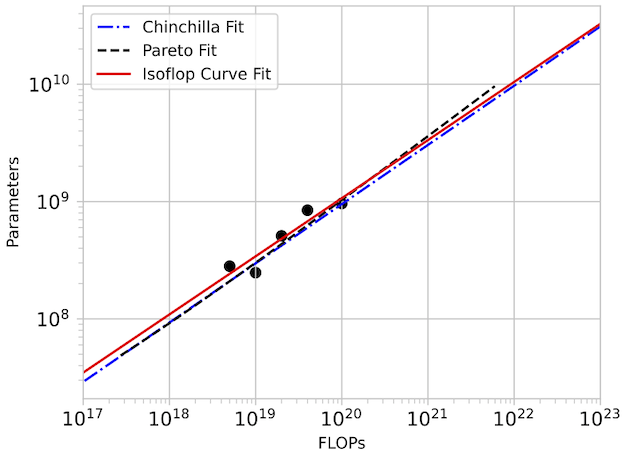
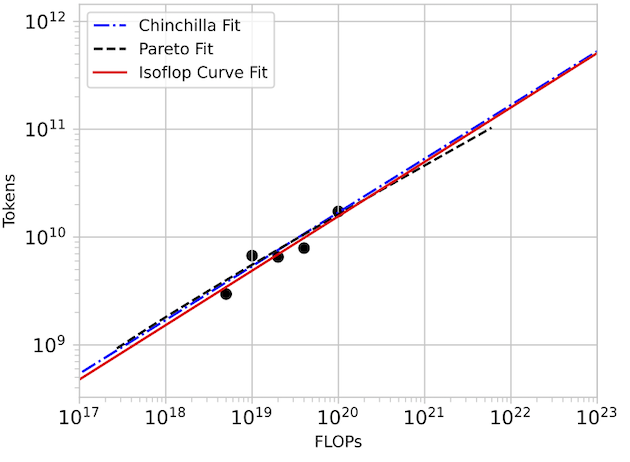
We reproduce the groundbreaking scaling laws results from DeepMind’s Chinchilla paper by simply running CARBS to tune the performance of GPT-like Transformers on the C4 dataset. We compare our predicted scaling laws with those reported in the Chinchilla paper and find that our predictions match exactly.

In detail: We set out to replicate the “approach 2” proposed in the Chinchilla paper by taking isoflop slices from our pool of observations. A linear fit to the minima of each of these isoflop curves yields $a=0.50$ for $N_{\rm opt}\propto C^a$ and $b=0.50$ for $D_{\rm opt}\propto C^b$. The Chinchilla results using the C4 dataset (see their Table A2) also give $a = 0.50$ and $b= 0.50$.

For our investigation, CARBS observed 340 training runs with models ranging from 19M to 1.5B parameters. Through this process, we simultaneously tuned 19 different parameters including regularization terms, schedule, model size, and token count, and we obtained the Chinchilla scaling result as a byproduct. By comparison, Chinchilla’s analysis required training 50 models ranging from 44M to 16B parameters (see their Table A9) with 9 different learning rate schedules/number of training tokens and held all other hyperparameters fixed. Given that Chinchilla looked at models up to 10x bigger and also performed more runs, we conclude that the CARBS analysis required less compute despite also marginalizing over many other hyperparameters and obtaining scaling relationships for each of them as well.

Demo 2 (Reinforcement Learning): A simple baseline tuned with CARBS solves most of ProcGen

Reinforcement learning algorithms are notoriously difficult to tune as they have many hyperparameters, including cost-influencing parameters such as the number of parallel environments, the number of passes over the data, and the network width. We empirically demonstrate that on challenging open problems such as OpenAI’s ProcGen suite, running CARBS on one of the simplest baselines, PPO ⁹ , leads to solving nearly the entire benchmark.

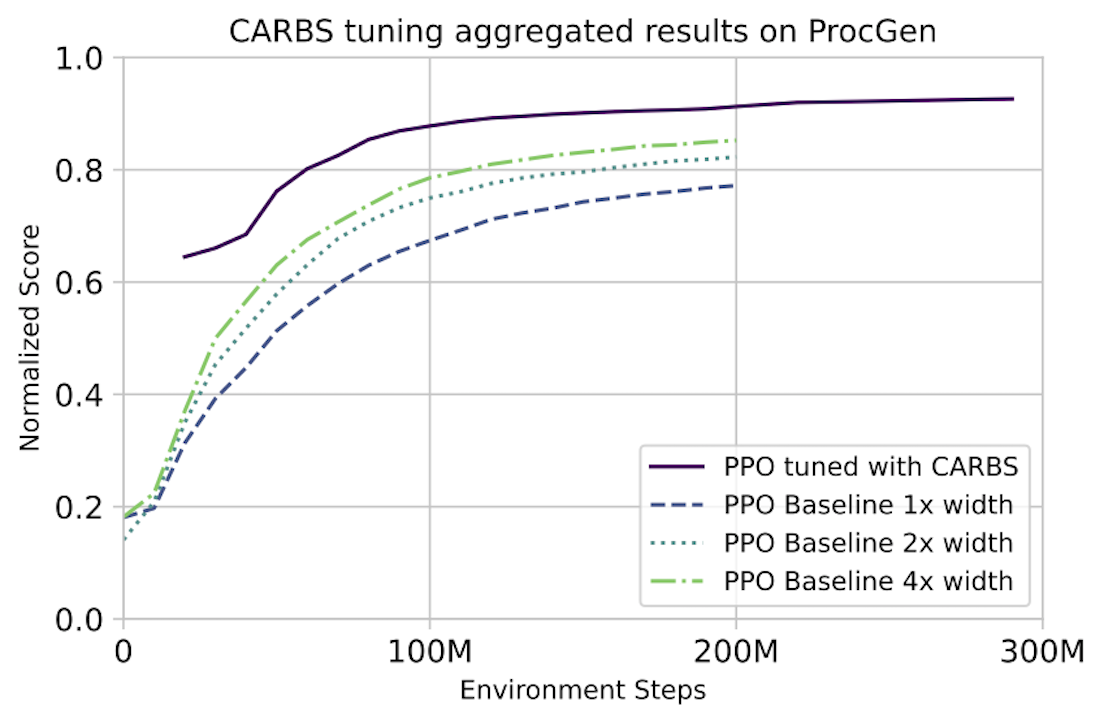
In detail: We use CARBS to tune a PPO baseline on each of the 16 tasks of the ProcGen benchmark. The results from the ProcGen paper are still the best-performing published PPO hyperparameters, so we use that as our baseline. We also include the 2x and 4x width configurations as additional baselines. We note that all of these baselines were still tuned by the original authors—just not with CARBS. In the plots below, we normalize the scores to the maximum theoretical score on each task, although a perfect score is not necessarily actually achievable for all tasks. The results are shown below.

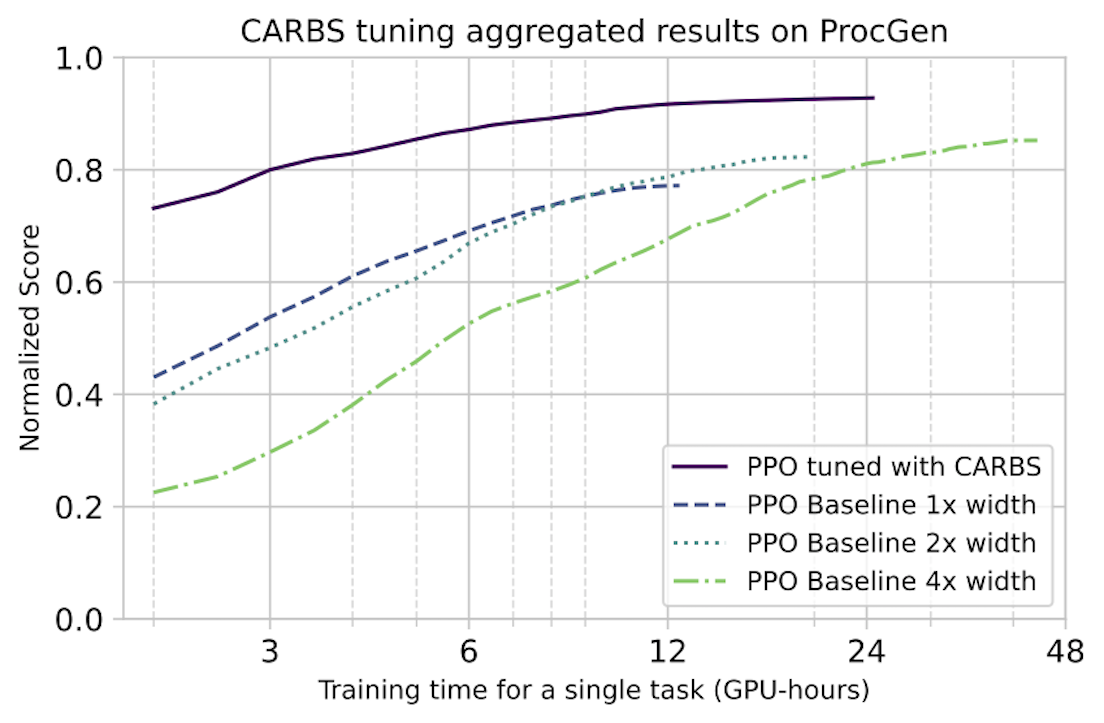
Top: Normalized score vs. training time in GPU-hours. These results show that CARBS-tuned PPO achieves the same performance with 4x less cost and performs >16% better than the previous SOTA.

Bottom: Normalized score vs. environment steps. ProcGen is typically trained for 200M steps. Although we do not explicitly search for algorithms with improved sample efficiency, we are able to use the observations from our tuning results to construct another Pareto curve trading off performance with number of environment steps. These results show that CARBS-tuned PPO can achieve the same performance with 1.5-4x less data.

We find that CARBS dramatically improves both performance and training cost on all tasks that are not already solved by the baseline (all but 3), in many cases fully or nearly solving them. For the 3 tasks that are solved by the baseline, CARBS significantly reduces the time required to solve the task. To the best of our knowledge, this CARBS-tuned PPO beats all other state of the art results on ProcGen.

Our hopes for CARBS

We created CARBS to accelerate our research through rigorous hyperparameter tuning and enable more robust science that builds on consistently well-tuned baselines. To learn more about CARBS, check out our preprint. To cite, use the following:

@ARTICLE{Fetterman++23,
       author = {{Fetterman}, Abraham J. and {Kitanidis}, Ellie and {Albrecht}, Joshua and {Polizzi}, Zachary and {Fogelman}, Bryden and {Knutins}, Maksis and {Wr{\'o}blewski}, Bartosz and {Simon}, James B. and {Qiu}, Kanjun},
        title = "{Tune As You Scale: Hyperparameter Optimization For Compute Efficient Training}",
      journal = {arXiv e-prints},
         year = 2023,
       eprint = {2306.08055},
}

If you are interested in building tools that enable scientific exploration, we’re always hiring!